Lecture 01 2018/01/17
1 Hello World
All code lives inside of classes, each file should have a public class that is has the same name with the file itself
Main function
- Syntax:
1
2
3
4
5public class <ClassName> {
public static void main(String[] args) {
//Function body here;
}
} - The main function can be regarded as the entrance to the program
- Syntax:
Use curly braces to denote the beginning and ending of the code
Statements should end with semi-colons
2 Running a Java Program
- Java complier:
javac, Java interpreter:java - Syntax:
javac xxx.java,java xxx - Procedure:
1
// source file: xxx.java => javac xxx.java => binary file: xxx.class => java xxx => execution results
- Notice: the source file name should be the same as the name of the public class contained inside it
- Why binary file is needed:
- It's type checked, to it's safer
- It's simpler for machine to execute the binary file, so it's faster
- Protect intellectual property, you don't need to give the original source file
3 Variables and Loops
- A variable should be declared with its type before it's used
- You can use while loop, for loop, for each loop or other loops
4 Gradscope course code: MNXYKX
5 Static Typing
- All variables and expressions have a static-type, the type cannot be changed
- Java complier performs a static type check, if there is an error in the source code, then the program is rejected before it even runs. While Python is a dynamically typed language, it runs until an error occurs
6 Defining Functions
Functions should be defined inside classes, we can call them methods
Here we only use static function
- Syntax:
1
2
3
4
5public class Test {
public static <return type> <function name> (<formal parameters>) {
//function body;
}
}
- Syntax:
Functions in Java can have at most one return values, but functions in Python can return multiple values
7 Code Style, Comments, Javadoc
- Good coding style:
Consistent styles(spacing, variable naming, brace style, etc)
Size(lines are not two wide, source files are not too large)
Description naming(variables, functions, classes)
Comments where appropriate
- Line comment
// Comments - Multi-line comments:
1
2
3/*
Comments
*/ - Javadoc:
1
2
3/**
* Comments
* /
- Line comment
- Comments:
- Methods, classes and variables should be described using Javadoc
format
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24// Class comments:
/**
* @author First Name Last Name <address@example.com>
* @version Version number
* @ since First compatible version number
*
*/
public class Test {
/**
* One line description
*
* Detailed description
*
* @param Parameter Name Description of parameter
*
* @return Describe the return value
*
*/
public static void main(String[] args) {
/** Description of variable x */
int x = 0;
// Function body;
}
}
- Methods, classes and variables should be described using Javadoc
format
Lab 01
1 Version Control Systems(VCSs):
- Version control systems are tools to keep track of changes to files over time
- Categories:
- Local VCS(LVCS): copy files into another directory
- Centralized VCS(CVCS):
- One server with all versioned files
- All clients checkout files from the central server
- May be affected by single point of failure
- Examples: CVS, Subversion, Perforce
- Distributed VCS(DVCS):
- One server, multiple clients, all have versioned files
- If the server dies, it can copy files from an arbitrary client to restore
- Examples: Git, Mercurial, Bazaar, Darcs
2 Git Local Repository:
git init: initiate a repositorygit add <file/directory>: add a file/directory to list of files to track, the terminology is called to stage a filegit commit -m "Message" <file/directory>: store a snapshot to the added files into the repositorygit log: show git commit logsgit show <object>: for commits, show the commit messages and textual diff1
// untracked files => git add => tracked files: unmodified/modified/staged
git reset <file/directory>: unstage a file/directorygit commit --amend: change commit messages or add forgotten filesgit checkout --<file/directory>: revert a file to its most recently committed version
3 Git Remote Repository:
git push <remote repo name> <remote repo branch>: push local repository to remote repository, for example,git push origin mastergit clone <remote repo url>: copy remote repository to local repositorygit remote add <remote repo name> <remote repo url>: add a remote for the repositorygit remote -v: list all remotes for the repogit remote add <short name> <remote url>: add a remote, the short first short name is usually calledorigingit remote rename <old short name> <new short name>: rename a remotegit remote rm <short name>: remove a remotegit clone <remote url>: clone a remote repository to local repositorygit clone <remote url> <directory name>: clone a remote repository to a specific directoryfetch: download but not merge,pull=fetch+merge
4 Git Branching:
- Reasons:
- Be prepared for dramatic changes(called refactoring)
- Separate works from others
- Leave space for possible incompatible program features
- Commands:
git branch <branch name>: create a new branchgit checkout <branch name>: switch to a specific branchgit checkout -b <branch name>:create a new branch and switch to itgit branch -d <branch name>: delete a branchgit branch -v: show current branch name
HW 00
1 Condition:
- If Statement:
Syntax:
1
2
3if(<boolean condition>) {
// Do something here;
}If no curly braces are used, then only the first statement after the boolean condition is regarded as inside the if statement
Curly braces:
1
2
3
4
5
6
7
8
9// Allman style/BSD style(in honor of Eric Allman)
if(<boolean condition>)
{
// Do something here;
}
//k&R style(in honor of Kernighan & Ritchie)
if(<boolean condition>) {
// Do something here;
}
2 Else Statement:
- Syntax:
1
2
3
4
5if(<boolean condition>) {
// Do something here;
} else {
// Do something here;
}
3 While Loop:
- Syntax:
1
2
3
4
5int counter = <start value>;
while(<boolean condition>) {
// Do something here;
//Change the counter;
}
4 Data Type in Java:
- Data type in Java:
byte,short,char,int,long,float,double,boolean(true,false),Object - There are typecasts among different types, and transformation from a more general type to a smaller type will lose precision
5 Array:
Initialize an array:
<type>[] <name> = new <type>[length];, For example,int[] values = new int[10];. There is also another way:int[] values = {1, 2, 3};Upon initialization using the first way, an array will be filled with default values. For an numeric array, it will be filled with
0, for a boolean array, it will be filled withfalse, for an object array, it will be filled withnullLength of an array:
<name>.lengthSort an array in place:
1
2import java.util.Arrays;
Arrays.sort(<array name>); //This method sort returns nothing(void)Higher-dimension array:
- Initialize an higher-dimension array example:
int[][] values = new int[3][4];
- Initialize an higher-dimension array example:
6 For Loop:
- Syntax:
1
2
3for(<initialization>; <termination>; increment){
// Do something here;
}
7 Break and Continue:
break;: terminate the innermost loopcontinue;: skip the current iteration of the loop and jump to the increment
8 The Enhanced For Loop:
- Syntax:
1
2
3for(<type> ele: <collections>) {
// Do something here;
}
Lecture 02 2018/01/19
1 Static v.s. Non-Static Methods:
Static methods:
- If class uses methods in class B, then class A is a client class of class B.
- Two ways to run methods in a class:
- Run methods in
mainfunction in its own class - Run methods in
mainfunction of a client class
- Run methods in
Instance variables and object instantiation
Objectis an instance of every class- Instance variables, a.k.a. non-static variables, are defined within a class
- Instance methods, a.k.a. non-static methods, are ones associated with instances
newis used for instantiation- Class methods, a.k.a. static methods, are accessed using dot notation
Constructor in Java:
- No return type, the name should be the same as the class name
- Syntax:
1
2
3
4
5
6public class <ClassName> {
// Constructor
public <ClassName> (<formal parameters>) {
this.<instance field> = parameter;
}
}
Array Instantiation, Arrays of Objects:
- Syntax:
1
<ClassName>[] <array name> = new <ClassName>[length];
- Syntax:
2 Class Methods v.s. Instance Methods:
- Class methods, a.k.a. static methods, are actions taken by class
itself. They are invoked by the class name:
<class name>.<static method name> - Instance methods, a.k.a. non-static methods, are actions taken a
specific instance of a class. They are invoked by a class instance:
<instance name>.<non-static method name> - Static variables: properties inherent to the class itself, usage:
<class name>.<static variable name>
3 public static void main(string[] args):
- The
mainfunction is called by the Java interpreter - The
argsare usually refereed to the command line arguments
4 Using Libraries:
- It will save you bunch of time and energy
Lecture 03 2018/01/22
1 Bits:
- Information in memory are 1s and 0s.
- 8 primitive types:
byte,short,char,int,long,float,double,boolean(true,false)
2 Declare a Variable in Primitive Type:
- Syntax:
type name;, e.g.int x; - Procedure:
- Computer sets aside enough bits to hold a thing of that type
- Java creates an internal table to map a variable to a location
- Java does not write anything in the reserved boxes if there is no assignment
3 The Golden Rule of Equals(GRoE):
y = xsimply copies the bits of x into the box of y- The rule applies to both primitive values and reference type objects
4 Reference Type:
- Object instantiation with
new:- Java allocates a box of bits for each instance variable of the class and fills them with a default value for the variable type(0, false, null)
- The constructor fills each box with formal parameters if there exists any
- You can think that
newreturns the location in memory where the instance is put
- Declaration of reference type:
- Java allocates a box of 64 bits, no matter what exactly the reference type object is
- The bits set to null(all 0s) or the 64-bit address returned by the
newstatement - If you reassign a variable to the another object, then the original objet is no longer being referred, if there is no other references, it will be garbage collected
5 Parameter Passing:
- GRoE applies in parameter passing, so the parameter passing is called the pass by value
- An example:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20public class PassByValueFigure {
public static void main(String[] args) {
Walrus walrus = new Walrus(3500, 10.5);
int x = 9;
doStuff(walrus, x);
/*
Pass by value, so the parameter W is the 64-bit address of walrus, and x is the bits of int 9,
in the local scope, when W.weight is changed, it also changes the referred object walrus,
but when the bits of int 9 is changed, is has no influence on the x in the outer scope.
*/
System.out.println(walrus.weight); // 3400
System.out.println(x); // 9
}
public static void doStuff(Walrus W, int x) {
W.weight = W.weight - 100;
x = x - 5;
}
}
6 The IntList class:
A comparison
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15public int size() {
if (this.rest == null) { // Here you cannot write like if(this == null ){ return 0;}, because it is an instance method,
return 1; // it's invoked by lst.size(), if lst == null, then this call will result in NullPointer error
}
return 1 + this.rest.size();
}
public static int size(IntList lst) {
if(lst == null) { // For the static method, you can use however, the lst == null statement, because in this situation,
return 0; // it's invoked by IntList.size(lst)
} else {
return 1 + size(lst.rest)
}
}If you use something like
this = this.restin your code, it's better to declare aheadIntList cur = thisand usecurinsteadOther functions:
size,iterativeSize,get
Lecture 04 2018/01/24
1 Improvements of the IntList into the
SLList:
Re-branding: rename to
IntListclass to theIntNodeclassBureaucracy:
- Put
IntNodeclass inside theSLListclass, hide the naked recursive structure in theIntNodeclass - add method:
addFirst,getFirst,addLast,size
- Put
Private v.s. Public:
- Private variables/methods cannot be accessed from somewhere outside the java file where they are defined
- in real world, private codes should be ignored by users, whereas public codes could be accessed and used from all users from anywhere
Nested classes:
Classes in different files can be put together into nested classes into a single file
If the nested class doesn't need access to other instance variables and methods, it could be declared as
staticUse a helper function when inner class is recursive structure, but the outer one is not
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19private static int sizeHelper(IntNode cur) {
if(cur.next == null) {
return 1;
} else {
return 1 + sizeHelper(cur.next);
}
}
/* This function is wrong, since there is no such function called size() in the inner InterNode class.
public int size() {
if(cur.next == null) {
return 1;
} else {
return 1 + node.next.size(); => this call is wrong
}
}
*/
public int size() {
return sizeHelper(node);
}Functions with same name but different signatures are called overloaded functions
Caching:
- Use a variable to cache the list size will result in quicker size function, but lower in addFirst function, addLast function and heavier memory usage
- The empty lists:
- The first way: use a new constructor for the empty list, in this way you need to take care of the null boundary condition
- Use sentinel node as a instance variable to calculate store the
first dummy node, the first actual node is
sentinel.next, this way is preferred for simpler boundary conditions
- Invariants:
- An invariant is a condition that is guaranteed to be true during code execution
- Invariants for the
SLListclass:- The first item is the
sentinel.next.first - The size is the actual amount of items
- Sentinel references refer to a sentinel node
- The first item is the
Lecture 05 2018/01/26
1 Improvements of the SLList into the
DLList:
Looking back:
- The addLast function is slow for the SLList, you can add a
public IntNode prevto convert the SLList(single-linked list) into the DLList(double-linked list) - Add a last node
private IntNode prev
- The addLast function is slow for the SLList, you can add a
Sentinel Update:
- Deal with the problem that last node can point to both a sentinel node or a real node
- The first way: use two sentinel nodes, one at the beginning of the list, one at the end of the list
- The second way: use one sentinel node, but let the list become circular, which means the last real node points to the sentinel node at the beginning
Generic lists:
- Deal with the problem that the current DLList can only holds int values
- Syntax:
1
2
3
4
5
6
7
8
9
10
11
12
13
14public class DLList<T> { // This means the DLList can hold type T values
private IntNode sentinel;
private int size;
public class IntNode {
public IntNode prev;
public IntNode next;
public T first; // The first item in the IntNode is type T
}
// Other codes
}
//The type in the new statement can be omitted, although it's definitely right to add it in the statement
DLList<String> lst = new DLList<>("String values");
2 Array Basics:
An array is a special type of object ths consists of a numbered sequence of memory boxes
Fixed integer length \(N\), then \(N\) boxes with indices starting from \(0\) to \(N - 1\), get length of an array:
myArray.lengthCreation:
int[] x = new int[3];int[] x = new int[] {1, 2, 3};int[] x = {1, 2, 3};
Access and Modification:
myArray.length;- Same object
array1 = array2; - Create a new object:
System.arraycopy(old_array, start_old_index, new_array, start_new_index, copy_length);
2D Arrays in Java:
- Example:
int[][] x = new int[4][];
- Example:
Arrays v.s. Classes:
- Both can be used to organize a bunch of memory boxes
- Array boxes are numbered and accessed by
[], class boxes are named(fields) and accessed by. - Array boxes should be in the same type, class boxes can be in different types
- One can specify array indices at runtime, and can only use reflection to specify class fields
Lecture 06 2018/01/29
1 DLList: fast in add/remove/get methods, ignore special cases, but get is slow for long lists, because you need to travel through every item on the way, which is slower than arrays in this sense, so we can use AList to tackle this problem
2 Resize AList when full, i.e., when
size == items.length:
The most trivial way:
1
2
3
4
5
6
7
8// Part of the addLast function with resizing taken into consideration
if (size == items.length) {
int[] newItems = new int[size + 1];
System.arraycopy(items, 0, newItems, 0, size);
newItems[size] = value;
size += 1;
items = newItems;
}The above way is quite slow when one adds a large quantity of items into the array, because there is so many resizing during the process
A faster way is called the multiplicative resizing:
items.length * multiplicative factor
3 Load factor/usage ratio
- Definition:
LF = size / items.length - If \(LF < 0.25\), then there is
so much space unused in the array, so we resize downwards the array by
items.length => items.length / 2
4 Genetic arrays:
Add a type generic to the AList so it can hold items other than integers
Syntax:
1
2
3
4
5// This is correct
Type[] items = (Type[]) new Object[capacity];
// This is wrong
Type[] items = new Type[capacity];One is not allowed to create generic type arrays in Java, one needs to use the typecast, otherwise a generic array creation error is caused
Lab 03
1 Unit Testing:
- Test each method in your code, and ultimately ensure that you have a working program
- Unit: break down the program into smallest part to enforce good code structure, each method should do only one thing
- JUnit: a unit testing framework for Java
2 Add JUnit to your program:
- Java program:
import org.junit.Test,import static org.junit.Assert.* - Maven program:
1
2
3
4
5<dependency>
<groupId>junit</groupId>
<artifactId>junit</artifactId>
<version>4.12</version> <!-- Enter a compatible junit version number here -->
</dependency>
For compatible versions, search search.maven.org
3 JUnit Syntax:
Syntax:
1
2
3
4
5
6
7
8
9
10
11public class ClassTest {
public void methodTest {
assertEquals(ExpectedValue, MethodCalculation);
assertNull(MethodCalculation); // This one equals to assertEquals(null, MethodCalculation);
assertTrue(MethodCalculation);
assertFalse(MethodCalculation);
assertNotEquals(ExpectedValue, MethodCalculation);
}
}Use annotation
@Testand non-static method only
4 Reverse a linked list:
Recursion:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18public class Test {
public static void reverse(LinkedNode first) {
if (first == null || first.next == null) { // Situation where the list is an empty linked list or there is only one item in the list
return first;
} else {
LinkedNode re = Test.reverse(first.next); // re is the reversed linked list,
first.next.next = first; // Let the second item in the linked list points to first
first.next = null; // Let first points to null
return re; // Return the whole reversed linked list
}
}
}
/* An example
LinkedList(1,2,3,4) => 1 -> 2 -> 3 -> 4 -> null
first = 1, re = LinkedList(4,3,2) => 4 -> 3 -> 2 -> null
first.next = 2, so the first.next.next = first turns re into 4 -> 3 -> 2 -> 1
first.next = null turns re into 4 -> 3 -> 2 -> 1 -> null, then done
*/Iteration:
1
2
3
4
5
6
7
8
9
10
11
12
13public class Test {
public static void reverse(LinkedNode first) {
LinkedNode re = null; // This is the reversed linked list
LinkedNode cur = first; // This is the first node in the unreversed part of the original list
while (cur != null) {
LinkedNode temp = cur.next; // Save the next node of the current node
cur.next = re; // current node points to first node in the reversed linked list
re = cur; // Modify the linked list to the current node is the first node in it
cur = temp; // Next node in the unreversed part of the original list
}
return re; // Return the whole reversed linked list
}
}
5 int and Integer:
- If two
intvariables have the same value, then they are equal - If two
Integervariables have the same value, then they may be not equal:1
2
3
4
5int a = val;
Integer val1 = Integer.valueOf(a);
Integer val2 = Integer.valueOf(a);
val1 == val2;
If \(0 \leq val \leq 127\), then
true, else if \(128 \leq
val\), then false. This is related to wrapper class
and java constant pool.
Project 01A
1 Dequeue: double ended queue, one can insert and delete from both sides
2 LinkedList implementation:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
public class LinkedListDeque<T> {
private TNode sentinel;
private int size;
public LinkedListDeque() {
sentinel = new TNode((T) Integer.valueOf(1), null, null);
sentinel.next = sentinel;
sentinel.prev = sentinel;
size = 0;
}
public int size() {
return size;
}
public void addFirst(T item) {
TNode temp = sentinel.next;
TNode newNode = new TNode(item, temp, sentinel);
sentinel.next = newNode;
temp.prev = newNode;
size += 1;
}
public void addLast(T item) {
TNode temp = sentinel.prev;
TNode newNode = new TNode(item, sentinel, temp);
sentinel.prev = newNode;
temp.next = newNode;
size += 1;
}
public boolean isEmpty() {
return size == 0;
}
public void printDeque() {
TNode cur = sentinel;
while (cur.next != sentinel) {
cur = cur.next;
System.out.print(cur.item + " ");
}
}
public T removeFirst() {
if (size == 0) {
return null;
}
TNode temp = sentinel.next;
sentinel.next = temp.next;
temp.next.prev = sentinel;
size -= 1;
return temp.item;
}
public T removeLast() {
if (size == 0) {
return null;
}
TNode temp = sentinel.prev;
sentinel.prev = temp.prev;
temp.prev.next = sentinel;
size -= 1;
return temp.item;
}
public T get(int index) {
int count = 0;
TNode cur = sentinel;
while (cur.next != sentinel) {
cur = cur.next;
if (count == index) {
return cur.item;
}
count += 1;
}
return null;
}
private T getHelper(int index, TNode cur, int count) {
if (index == count) {
return cur.item;
}
return getHelper(index, cur.next, count + 1);
}
public T getRecursive(int index) {
return getHelper(index, sentinel.next, 0);
}
private class TNode {
public T item;
public TNode next;
public TNode prev;
public TNode(T item, TNode next, TNode prev) {
this.item = item;
this.next = next;
this.prev = prev;
}
}
}
3 Array implementation:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
public class ArrayDeque<T> {
private T[] items;
private int initialCapacity = 8;
private double usageFactor = 0.25;
private int front;
private int rear;
public ArrayDeque() {
items = (T[]) new Object[initialCapacity];
front = -1;
rear = -1;
}
public int size() {
/*
Two conditions to calculate the dequeue size:
If front < rear: then size = rear - front + 1
If front > rear: then size = rear - front + 1 + n
*/
if (front < 0 || rear < 0) {
return 0;
}
return (rear + 1 - front + items.length) % items.length;
}
private boolean isFull() {
/*
Two conditions for a dequeue implemented in circular array to be full:
If front < rear: then front == 0 && rear == items.length -1
If front > rear: then front - rear == 1
*/
return (rear + 1) % items.length == front;
}
public boolean isEmpty() {
return front == -1 && rear == -1;
}
private void expandLength() {
int temp = items.length;
T[] newItems = (T[]) new Object[items.length * 2];
System.arraycopy(items, 0, newItems, 0, items.length);
items = newItems;
front = 0;
rear = temp - 1;
}
private void reduceLength() {
T[] newItems = (T[]) new Object[items.length / 2];
int temp = size();
if (front < rear) {
System.arraycopy(items, front, newItems, 0, size());
} else if (front > rear) {
System.arraycopy(items, front, newItems, 0, items.length - front);
System.arraycopy(items, 0, newItems, items.length - front, rear + 1);
}
items = newItems;
front = 0;
rear = temp - 1;
}
public void addFirst(T item) {
if (isFull()) {
expandLength();
}
if (front < 0) { // Empty dequeue
front = 0;
rear = 0;
} else if (front == 0) { // Front is at index 0
front = items.length - 1;
} else { // Other situations
front -= 1;
}
items[front] = item;
}
public void addLast(T item) {
if (isFull()) {
expandLength();
}
if (rear < 0) { // Empty dequeue
front = 0;
rear = 0;
} else if (rear == items.length - 1) { // Rear is at index items.length - 1
rear = 0;
} else { // Other situations
rear += 1;
}
items[rear] = item;
}
public T removeFirst() {
if (items.length >= 16 && size() * 1.0 / items.length < usageFactor) {
reduceLength();
}
if (front < 0) { // Empty dequeue
return null;
} else if (front == rear) { // Only one item in the dequeue
T temp = items[front];
items[front] = null;
front = -1;
rear = -1;
return temp;
} else if (front == items.length - 1) { // Front is at index items.length - 1
T temp = items[front];
items[front] = null;
front = 0;
return temp;
} else { // Other situations
T temp = items[front];
items[front] = null;
front += 1;
return temp;
}
}
public T removeLast() {
if (items.length >= 16 && size() * 1.0 / items.length < usageFactor) {
reduceLength();
}
if (rear < 0) { // Empty list
return null;
} else if (rear == front) { // Only one item in the dequeue
T temp = items[rear];
items[rear] = null;
rear = -1;
front = -1;
return temp;
} else if (rear == 0) { // Rear at index 0
T temp = items[rear];
items[rear] = null;
rear = items.length - 1;
return temp;
} else { // Other situations
T temp = items[rear];
items[rear] = null;
rear -= 1;
return temp;
}
}
public void printDeque() {
if (front < rear) {
for (int i = front; i < rear + 1; i++) {
System.out.print(items[i] + " ");
}
} else if (front > rear) {
for (int i = front; i < items.length; i++) {
System.out.print(items[i] + " ");
}
for (int i = 0; i <= rear; i++) {
System.out.print(items[i] + " ");
}
} else {
System.out.print(items[front] + " ");
}
}
public T get(int index) {
if (isEmpty() || index < 0 || index > size() - 1) {
return null;
}
/*
Two conditions for the index:
If front < rear: then front = 0 and index starts from 0, the index can be used directly
If front > rear: then we want index 0 to be items[front], let index = (front + index) % items.length
*/
index = (front + index) % items.length;
return items[index];
}
}
Lecture 07 2018/01/31
1 Testing and Selection Sort
- Testing
- In the real world, programmers believe their code works because of tests they write themselves
- Ad Hoc Testing v.s. Junit
- Ah Hoc Testing:
- Write test yourself, but test code can have bugs
- Java implementation demo:
1
2
3if (Arrays.equals(input, expected)) {
System.out.println("Oooops! There occurs a problem!");
}
- Ah Hoc Testing:
- Junit testing:
- Remove tedious code, and leave no room for errors in manually written testing code
- Java demo:
1
2org.junit.Assert.assertEquals(expected, input);
org.junit.Assert.assertArrayEquals(expected, input);
- Selection sort
- Selection sorting a list of N items:
- Find the smallest item
- Move it to the front
- Selection sort the remaining items without touching front item
- Java implementation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31public class SelectionSort {
// find the smallest item
private static int findSmallestIndex(String[] items, int start) {
int smallestIndex = start;
for (int i = smallestIndex; i < items.length; i++) {
if (items[i].compareTo(items[smallestIndex]) < 0) {
smallestIndex = i;
}
}
return smallestIndex;
}
// move it to the front
private static void swap(String[] items, int a, int b) {
String item = items[a];
items[a] = items[b];
items[b] = item;
}
// selection sort the remaining items
private static void sort(String[] items, int start) {
if (start == items.length) {
return;
}
int smallestIndex = findSmallest(items, start);
swap(items, start, smallestIndex);
sort(items, start + 1);
}
public static void sort(String[] items) {
sort(items, 0);
}
}
- Selection sorting a list of N items:
- Simpler JUnit
- Test annotation:
- Precede each method with
@org.junit.Test - Change each test method to be non-static
- Remove main method with static methods
- Precede each method with
- Advantages:
- No need to manually invoke tests
- All tests are run, not just the ones we specify
- If one test fails, the others still run
- A count of how many tests were run and how many passed is provided
- The error messages on a test failure are much nicer looking
- If all tests pass, we get a nice message and a green bar appears, rather than simply getting no output
- Test annotation:
- Testing Philosophy
- Correctness Tool #1: Autograder
- Correctness Tool #2: JUnit Tests
- Test-Driven Development (TDD):
- Steps:
- Identify a new feature
- Wriate a unit test for that feature
- Run the test. It should fail
- Write code that passes the test
- Optional: refactor code to make it faster, cleaner, etc
- Identify a new feature
- Steps:
- Correctness Tool #3: Integration Testing
Lecture 08 2018/02/02
1 Interfaces
- Method overloading
- Definition: multiple methods with same name, but different parameters/signatures
- Downsides of method overloading:
- It's super repetitive and ugly, because you now have two virtually identical blocks of code
- It's more code to maintain, meaning if you want to make a small change to the longest method such as correcting a bug, you need to change it in the method for each type of list
- If we want to make more list types, we would have to copy the method for every new list class
- Hypernym, Hyponym, and Interface Inheritance
- Hypernym and hyponym comprise a hierarchy
- Is-a relationship: an instance from hyponym is an instance from hypernym
- Interface: it specifies what a bunch of objects must be able to do, but it doesn't provide any implementation for those behaviors
- A class implements an interface, a class extends a class, an interface extends an interface
- Overriding
- If a subclass has amethod with the exact same signature as in the superclass, we say the subclass overrides the method
- Methods with the same name but different signatures are overloaded
- Override annotation:
@overridebefore the method signature- Even if you don't write override annotation, subclass still overrides the method
- Override annotation is an optional reminder that you're overriding
- Override annotation protects against typos
- Interface Inheritance
- The usage of the implements keyword is sometimes referred to as interface inheritance
- Polymorphism:
1
2
3
4
5public class A extends B {
public static void main(String[] args) {
A instance = new B();
}
}
- Implementation Inheritance
- By default, subclass inherits signatures, but not implementation
- For better or worse, java allows implementation inheritance, where subclasses can inherit signatures and implementation
- Use default keyword to specify a method that subclasses should
inherit from an interface
1
2
3
4
5
6public interface Test {
public String toString();
default public void done() {
System.out.println("Done!");
}
} - You can use override annotation and override the default method in an interface
- Static type v.s. dynamic type
- Static type: compile-time type, this is the type specified at
declaration, it never changes
- Dynamic type: run-time type, this is the type specified at instantiation(when using new), it equals to the type of the object being pointed at
- Dynamic method selection: if you call a method of an object using a variable with compile-time type X and run-time type Y, and if Y overrides the method, Y's method is then used instead
- This does not work for overloaded methods, when java checks to see
which overloaded method to call, it checks the static type and calls the
method with the parameter of the same type
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18public class A extends B {
public A() {
// do sth
}
public static void print(B item) {
System.out.println(item);
}
public static void print(A item) {
System.out.println(item);
}
A itemA = new A();
B itemB = itemA;
print(itemA); // this calls the print function with signature of item A
print(itemB); // this calls the print function with signature of item B
}
- Static type: compile-time type, this is the type specified at
declaration, it never changes
Lecture 09 2018/02/05
1 Extends
- Extends keyword
- If you want one class to be nyponym of another class, you use
extendskeyword - Subclasses inherit all members of the parent class, the members
include:
- All instance and static variables
- All methods
- All nested classes
- Constructors are not inherited, and private members cannot be directly accessed by subclasses
- You can use
superkeyword to call methods defined in the super class
- If you want one class to be nyponym of another class, you use
- Constructors are not inherited
- Java requires that all constructors must start with a call to one of its superclass's constructors
- Two ways to do this:
- If you do provide a constructor, its first line should call
constructors in the superclass:
1
2
3
4
5
6public class A extends B {
public A() {
super();
// do sth
}
} - If you do not explicitly provide a constructor, Java will automatically make a call to the superclass's no-argument constructor for us.
- If you want to call constructor other than the non-argument one in
the superclass, explicitly call it with the correct signature
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22public class B {
public String item;
public B() {
this.item = null;
}
public B(String item) {
this.item = item;
}
}
public class A extends B {
public A() {
super;
}
public A(String item) {
super(item);
}
}
- If you do provide a constructor, its first line should call
constructors in the superclass:
- The Object class
- Every class in Java is a descendant of the Object class, or extends the Object class. Even classes that do not have an explicit extends in their class still implicitly extend the Object class
2 Encapsulation
- Introduction
- Encapsulation is one of the fundamental principles of object oriented programming, and is one of the approaches that we use to deal with complexity
- Deal with complexity: *Hierarchical abstraction: create layers of abstraction, with clear abstraction barriers
- Design for change:
- Organize program around objects
- Let objects decide how things are done
- Hide information others don't need
- Module:
- Definition: a set of methods that work together as a whole to perform a task or set of related tasks
- A module is said to be encapsulated if its implementation is completely hidden, and it can be accessed only through a documented interface
- Abstraction barriers
- The private keyword builds the abstraction barriers
- Implementation inheritance breaks encapsulation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29public class Dog {
public void bark() {
barkMany(1);
}
public void barkMany(int N) {
for (int i = 0; i < N; i++) {
System.out.println("bark!");
}
}
}
public class VerboseDog extends Dog {
public void barkMany(int N) {
System.out.println("As a dog, I say: ");
for (int i = 0; i < N; i++) {
System.out.println("bark!");
}
}
public static void main(String[] args) {
VerboseDog dog = new VerboseDog();
// the following method call results in infinite loop
dog.barkMany(5);
}
}
3 Type Checking and Casting
- Dynamic method lookup
- Both variables and expressions have static type and dynamic type
1
2
3
4// wrong
Integer x = new Double();
// correct
Double x new Integer(); - Method calls have static type that equals to their declared type
1
2
3
4
5
6
7
8public Double maxVal(Integer x, Integer y) {
return x > y ? x : y
}
// wrong
Integer x = maxVal(5, 6);
// correct
Double x = maxVal(5, 6);
- Both variables and expressions have static type and dynamic type
- Casting
- Casting is a powerful but dangerous tool. Essentially, casting is telling the compiler not to do its type-checking duties
- Demo:
1
2
3
4
5public Double maxVal(Integer x, Integer y) {
return x > y ? x : y
}
Integer x = (Integer) maxVal(5, 6);
4 Higher Order Functions
- Introduction
- Definition: A higher order function is a function that treats other functions as data
- Python demo:
1
2
3
4
5
6
7
8def tenX(x):
return 10 * x
def doTwice(f, x):
return f(f(x))
if __name__ == '__main__':
print(doTwice(tenX, 10)) - Java demo:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20public interface IntFunction {
int apply(int x);
}
public class TenX implements IntFunction {
public int apply(int x) {
return 10 * x;
}
}
public class Test {
public static int doTwice(IntFunction f, int x) {
return f.apply(f.apply(x));
}
public static void main(String[] args) {
TenX tenX = new TenX();
System.out.println(doTwice(tenX, 10));
}
}
Lecture 10 2018/02/07
1 Subtype Polymorphism
- Introduction
- Polymorphism: provide a single interface to entities of different types
- Build an interface an implements to interface to compare
2 Comparable
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24public interface OurComparable {
public int compareTo(Object that);
}
public class OurClass implements OurComparable {
public int compareTo(Object that) {
if (that == null) {
throw new IllegalArgumentException("Null input!");
}
// casting can be dangerous: OurClass that = (OurClass) that;
if (!(that instanceof OurClass)) {
throw new IllegalArgumentException("Input type error!");
}
if (this.field.compareTo(that.field) > 0) {
return 1;
} else if (this.field.compareTo(that.field) < 0) {
return -1;
}
return 0;
}
}
- The interface
- Java implementation
1
2
3public interface Comparable<T> {
public int compareTo(T obj);
} - Usage: 3 Comparator
1
2
3
4
5
6
7
8
9
10
11
12public class OurClass implements Comparable<OurClass> {
public int compareTo(OurClass that) {
if (this.field.compareTo(that.field) > 0) {
return 1;
} else if (this.field.compareTo(that.field) < 0) {
return -1;
}
return 0;
}
}
- Java implementation
- Introduction
- Natural order: used to refer to the ordering implied in the compareTo method of a particular class
- If you want to use an order that is different from the natural order, you should implement the Comparator interface
- The interface
- Java implementation:
1
2
3public interface Comparator<T> {
int compare(T o1, T o2);
} - Usage:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27public class OurClass {
private static class OurComparator implements Comparator<OurClass> {
public int compare(OurClass a, OurClass b) {
if (a == null || b == null) {
throw new IllegalArgumentException("Null input!");
}
if (a.field.compareTo(b.field) < 0) {
return -1;
} else if (a.field.compareTo(b.field) == 0) {
return 0;
}
return 1;
}
}
public Comparator<OurClass> getComparator() {
return new OurComparator();
}
public static void main(String[] args) {
OurClass a = new OurClass();
OurClass b = new OurClass();
Comparator<OurClass> comparator = OurClass.getComparator();
System.out.println(comparator.compare(a, b));
}
}
- Java implementation:
Lecture 11 2018/02/09
1 Abstract Data Types(ADTS)
- Interface inheritance for comparison
- Specify a contract for common behaviro shared by mant data structures
- Provide a way to containerize common functions
- ADT
- An ADT is defined only by its operations, not by its implementation
- The Stack ADT:
push(T x)T pop()
- The GrabBag ADT:
insert(T x)T remove(): random removeT sample(): random sampleint size()
2 Java Libraries
- ADTs in the java.util library:
- List: an orderded collection of items, a popular implementation is the ArrayList
- Set: an unordered collection of strictly unique items(no repeats), a popular implementation is the HashSet
- Map: a collectoin of key/value pairs, you can access th value via the key, a popular implementation is the HashMap
- Inheritance hierarchy:
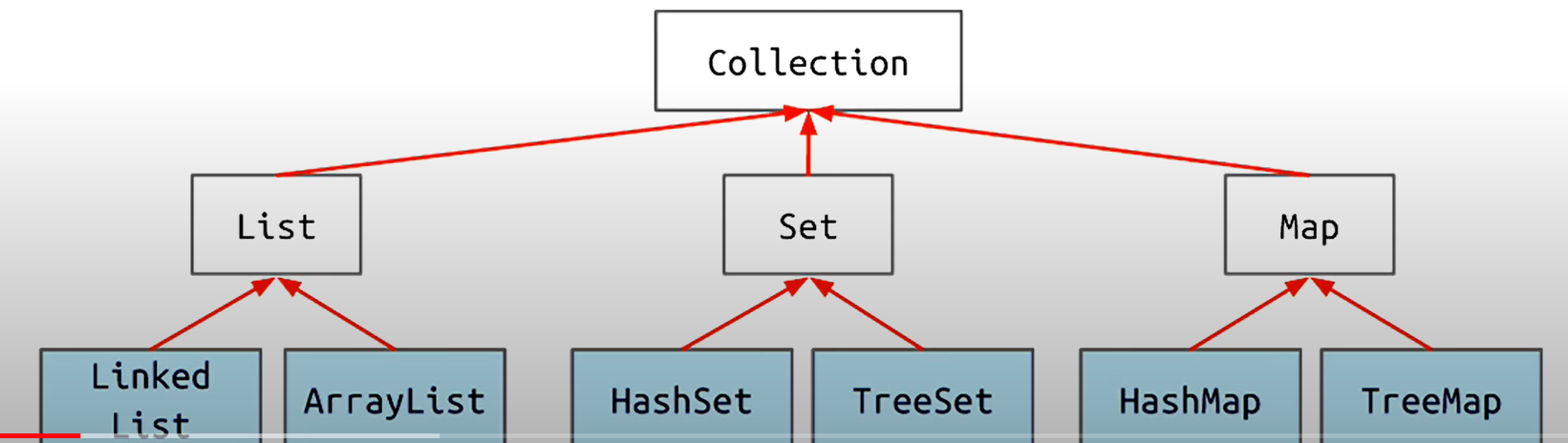
- Example: getwords into a list
1
2
3
4
5
6
7
8
9
10public class Test {
public static void main(String[] args) {
List<String> words = new ArrayList<String>();
In in = new In("file.type");
while (!in.isEmpty()) {
String word = in.readString();
words.add(word);
}
}
} - Example: count unique words in the list
1
2
3
4
5
6
7
8
9
10public class Test {
public static void main(String[] args) {
Set<String> wordSet = new HashSet<String>();
for (int i = 0; i < words.size(); i++) {
String word = words.get(i);
wordSet.add(word);
}
System.out.println(wordSet.size());
}
} - Example: given List
targets and List words, find the freqency of targets in the words 3 Abstract Classes1
2
3
4
5
6
7
8
9
10
11
12
13public class Test{
public static void main(String[] args) {
Map<String, Integer> wordMap = new HashMap<String, Integer>();
for (String target: targets) {
wordMap.put(target, 0);
}
for (String word: words) {
if (wordMap.containsKey(word)) {
wordMap.put(word, wordMap.get(word) + 1);
}
}
}
}
- Interfaces
- Cannot be instantiated
- Can provide either abstract or concrete methods
- Use no keyword for abstract methods
- Use default keyword for concrete methods
- Can provide only public static final variables
- Can provide only public methods
- Abstract Classes
- Cannot be instantiated
- Can provide either abstract or concrete methods
- Use abstract for abstract methods
- Use no keyword for concrete methods
- Can provide any kind variables
- Can provide any kind methods
- Comparisons
- Interfaces:
- Primiarily for interface inheritance, limited implementation inheritance
- Classes can implement multiple interfaces
- Abstract classes
- Can do anything an interface can do, and more
- Subclasses only extend one abstract classes
- Interfaces:
Lecture 12 2018/02/14
1 Automatic Conversions
- The syntax lectures
- Syntax 1: Autoboxing, promotion, immutability, generics
- Syntax 2: Exceptions, access control
- Syntax 3: Iterables/iterators, equals, other loose ends
- Syntax 4: Wildcards, type upper bounds, covariance
- Generics
- Generic classes require use to provide one or more actual type arguments
- Generic classes only accecpt reference types, no primitive types are allowed
- Conversion:
1
2Integer val = new Integer(intVal);
int intVal = val.valueOf(); - Autoboxing/autounboxing: in Java 1.5, conversions between primitive types and associated wrapper types are introduced
- Autoboxing/autounboxing does not apply for arrays
- Wrapper types use much more memory, and there is some performance loss
- Convert from String to primitive type
int val = Integer.parseInt(string)
- Primitive Widening
- If a program expects a primitive of type T2 and is given a variable of type T1, and type T2 can take on a wider range of values than T1, the the variable will be implicitly cast to type T2.
- Immutability
- An immutable data type is one for which an instance cannot change in any observable way after instantiation
- Example: ArrayDeque is mutable. Integer, String are immutable
- The final keyword will help the complier ensuer immutability:
- The final variable means you will assign a value once
- Not necessary to have final to be immutable(e.g. the private variables in a class cannot be changed from outside unless reflection is used)
- Advantage: less to think about, avoid bugs and makes debugging easier
- Disadvantage: must create a new objecct anytime anything changes
- Warning: declaring a reference as final does not make object
immutable
1
2public final ArrayDeque<String> d = new ArrayDeque<String>();
// this means d cannot point to another ArrayDeque, but the created ArrayDeque object can change
Lecture 13 2018/02/16
1 Lists, Sets
- Lists
1
2
3
4import java.util.List;
import java.util.ArrayList;
List<Integer> list = new ArrayList<>();
list.add(5);1
2ls = []
ls.append(5) - Sets
1
2
3
4import java.util.Set;
import java.util.HashSet;
Set<String> set = new HashSet<>();
set.add('a');1
2s = set()
s.add('a')
2 Exceptions
- Throw Exceptions
- Exceptions cause normal flow of control to stop. We can in fact choose to throw our own exceptions
- Java demo
1
2
3
4
5
6public void myFun(int arg) {
if (arg == null) {
throw new IllegalArgumentException("Null input!");
}
System.out.println(arg + 1);
} - Python demo
1
2
3
4
5
6def myFun(arg: int) -> None:
try:
print(arg + 1)
except ValueError:
print("Null input!")
3 Iteration
- Enhanced for loop
- Demo
1
List<Integer> list = new ArrayList<>();
- In order to support for-each loop, a class should implement iterable
interface and have an iterator method
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16public class Test<T> implements Iterable<T>{
public Iterator<T> iterator() {
return new MyIterator();
}
private class Iterator implements Iterator<T> {
public boolean hasNext() {
// do sth;
}
public T next() {
// do sth;
}
}
}
- Demo
Lecture 14 2018/02/21
1 Packages and Jar Files
- Package Introduction:
- A package is a namespace that organizes classes and interfaces
- Naming convertion: Package name starts with website address
- If used from outside, use the entire canonical name, if used from another class in the same package, you can just use the simple name
- Create a Package:
- Two steps:
- At the top of every file in the package, put the package name
- Make sure that the file is stored in a folder with the appropriate folder name
- Example: the
Dog.javain folderug/joshh/animal1
2
3
4
5package ug.joshh.animal;
public class Dog {
// do sth;
}
- Two steps:
- Use Packages:
- Use canonical name: to use a class from package A in a class from
package B, you can use the canonical name
1
new ug.joshh.animal.Dog dog = new us.joshh.animal.Dog();
- Use import statement
1
2import us.joshh.animal.Dog;
Dog dog = new Dog();
- Use canonical name: to use a class from package A in a class from
package B, you can use the canonical name
- The Default Package
- Any java class without a package name at the top are part of the "default" package
- Generally, you should not use the default package except for tiny small programs
- You cannot import code from the default package
- JAR files
- .jar file contains all of the .class files needed for your program
- Create a .jar file use IntelliJ:
- Go to File -> Project Structure -> Artifacts -> JAR -> From modules with dependencies
- Click OK a couple of times
- Click Build -> Build Artifacts(this will create a JAR file in a folder called "Artifacts")
- Distribute the JAR file to other programmers, who can now import it into IntelliJ
- JAR files are just zip files, they are easy to unzip and transform back into .java files
2 Access Control
Access Control with Inheritance and Packages
Modifier Class Package Subclass World Comment public Yes Yes Yes Yes accessible everywhere protected Yes Yes Yes No protected from outside world default/No modifier Yes Yes No No package-private private Yes No No No private from everything else The default package example
For the default package, because no modifier is provided on package information, everything is package-private, thus code in the default package cannot be accessed from user-defined package
Some Notes
- For interface, even if a method is unmodified, it is still public rather than package-private
- Access is based only on static types
Lecture 15 2018/02/23
1 Efficient Programming
- Two costs of efficienty
- Programming cost
- How long does it take to develop your program
- How easy is it to read, modify, and maintain your code
- Execution cost
- How much time does your program take to execute
- How much memory does your program require
- Programming cost
- Encapsulation
- Module: A set of methods that work together as a whole to perform some task or set of related tasks
- Encapsulated: A module is said to be encapsulated if its implementation is completely hidden, and it can be accessed only through a documented interface
- API
- Definition: an API(Application Programming Interface) of an ADT is the list of constructors and methods and a short description of each
- API consists of syntactic and semantic specification
- Compiler verifies that syntax is met
- Tests help verify that semantics are correct
- ADT
- Definition: ADT's (Abstract Data Structures) are high-level types that are defined by their behaviors, not their implementations.
Lecture 16 2018/02/26
1 Asymptotics I: An Introduction to Asymptotic Analysis
- Runtime Characterization
- Characterization should be simple and mathematically rigorous
- Characterization should clearly demonstrate the superiority of different programs
- Technique 1: measure execution time in seconds using a client
program
- Good: easy to measure, meaning is obvious
- Bad: may require large amounts of computation time, result varies with machine, complier, input data, etc
- Technique 2: count possible operations for an array of size N
- Good: machine independent, input dependence captured in model
- Asymptotic Behavior
- In most cases, we only care about asymptotic behavior, i.e. what happens for very large N
- Simplication 1: consider only the worst case when comparing algorithms
- Simplication 2: pick some representative operation(the one with largest orders) to act as a proxy for the overall runtime, this is called cost model
- Simplication 3: ignore lower order terms
- Simplication 4: ignore multiplicative constants
- Formalize Order of Growth
- Big-Theta Notation
- Used to describe the order of growth of a function
- Also used to describe the rate of growth of the runtime of a piece of code
- Big-Theta can be thought of something like "equals"
- \(R(N) \in \Theta (f(N))\) iff \(\exists \; k_{1} \; k_{2}\) such that \(k_{1} f(N) \leq R(N) \leq k_{2} f(N)\)
- Big-O Notation
- Big-O can be though of something like "less than or equal"
- \(R(N) \in O(f(N))\) iff \(\exists \; k_{2}\) such that \(R(N) \leq k_{2} f(N)\)
- Big-Theta Notation
Lecture 17 2018/02/28
1 Asymptotic Analysis II
- An example
1
2
3
4
5
6
7
8// This one is O(N)
public static void printParty(int N) {
for (int i = 0; i < = N; i = i * 2) {
for (int j = 0; j < i; j += 1) {
System.out.prinln("Hello");
}
}
} - Some math
- \(1 + 2 + 3 + ... + Q = Q * (Q + 1) / 2 = \Theta(Q^{2})\)
- \(1 + 2 + 4 + ... + Q = 2 * Q - 1 = \Theta(Q)\)
- Recursion
- Example
1
2
3
4
5
6
7// This one is O(2^N)
public static int f3(int n) {
if (n <= 1) {
return 1;
}
return f3(n-1) + f3(n-1);
}
- Example
- Binary Search
- Example
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31// The complexity of binary search is O(log_{2}N)
public static int binarySearch(String[] sorted, String x, int lo, int hi) {
if (lo > hi) {
return -1;
}
int m (lo + hi) / 2;
int cmp = x.compareTo(sorted[m]);
if (cmp < 0) {
return binarySearch(sorted, x, lo, m - 1);
} else if (cmp > 0) {
return binarySearch(sorted, x, m + 1, hi);
} else {
return m;
}
}
public static int recursiveBinarySearch(String[] sorted, String x) {
int lo = 0;
int hi = sorted.length();
while (low < hi) {
int m = (lo + hi) / 2;
int cmp = x.compareTo(sorted[m]);
if (cmp < 0) {
high = m - 1;
} else if (cmp > 0) {
lo = m + 1;
} else {
return m;
}
}
}
- Example
- Merge Sort
- Selection Sort
- Recursive version:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31public class SelectionSort {
// find the smallest item
private static int findSmallestIndex(String[] items, int start) {
int smallestIndex = start;
for (int i = smallestIndex; i < items.length; i++) {
if (items[i].compareTo(items[smallestIndex]) < 0) {
smallestIndex = i;
}
}
return smallestIndex;
}
// move it to the front
private static void swap(String[] items, int a, int b) {
String item = items[a];
items[a] = items[b];
items[b] = item;
}
// selection sort the remaining items
private static void sort(String[] items, int start) {
if (start == items.length) {
return;
}
int smallestIndex = findSmallest(items, start);
swap(items, start, smallestIndex);
sort(items, start + 1);
}
public static void sort(String[] items) {
sort(items, 0);
}
} - Iterative version:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15public class SelectionSort {
public static void sort(String[] items) {
for (int i = 0; i < items.length; i++) {
int minIndex = i;
for (int j = i; j < items.length; j++) {
if (items[j].compareTo(items[minIndex]) < 0) {
minIndex = j;
}
}
String item = items[i];
items[i] = items[minIndex];
items[minIndex] = item;
}
}
}
- Recursive version:
- Demo
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42public class MergeSort {
private static Comparable[] aux;
public static void sort(Comparable[] items) {
aux = new Comparable[items.length]; // Do not create aux in the private recursive sorts
sort(items, 0, items.length - 1);
}
private static void sort(Comparable[] items, int lo, int hi) {
if (hi <= lo) {
return;s
}
int mid = lo + (hi - lo) / 2;
sort(items, lo, mid);
sort(items, mid + 1, hi);
merge(items, lo, mid, hi);
}
private static void merge(Comparable[] items, int lo, int mid, int hi) {
// assert isSorted(items, lo, mid);
// assert isSorted(items, mid + 1, hi);
for (int i = lo; i <= hi; i++) {
aux[i] = items[i];
}
int i = lo; j = mid + 1;
for(int k = lo; k <= hi; k++) {
if (i > mid) {
items[k] = aux[j++]; // items[lo...mid] has already been copied
} else if (j > hi) {
items[k] = items[i++]; // items[mid + 1...hi] has already been copied
} else if (aux[j].compareTo(aux[i]) < 0) {
items[k] = aux[j++]; // For stability reason, we cannot revert this else if statement and the else statement
} else {
items[k] = aux[i++];
}
}
// assert isSorted(items, lo, hi)
}
}
- Selection Sort
Lecture 18 2018/03/01
- Runtime Analysis Subtleties
- When average case, best case and worst case are not in the same order, you can simply use Big O notation instead of Big Theta notation
- Big Theta is more informative because it has more precision
- Big Theta: "equal to", Big O: "less than or equal to", Big Omega: "greater than or equal to"
- Summary
| Information Meangin | Example Family | Example Family Members | |
|---|---|---|---|
| Big Theta: \(\Theta (f(M))\) | Order of growth is \(f(N)\) | \(\Theta (n^2)\) | \(\frac{N^2}{2},2N^2,N^2+38N+\frac{1}{N}\) |
| Big O: \(O(f(N))\) | Order of growth is less than or equal to \(f(N)\) | \(O(n^2)\) | \(\frac{N^2}{2},2N^2,logN\) |
| Big Omega: \(\Omega (f(N))\) | Order of growth is greater than or equal to \(f(N)\) | \(\Omega(n^2)\) | \(\frac{N^2}{2},2N^2,5^N\) |
Amortized Analysis
- Steps:
- Pick a cost model (like in regular runtime analysis)
- Compute the average cost of the i'th operation
- Show that this average (amortized) cost is bounded by a constant
- Equation
For each operation, let \(c_i\) be the true cost of the operation, let \(a_i\) be some arbitrary amortized cost, \(a_i\) is a positive constant for every operation.
Let \(\Phi_i\) be the potential at operation i, which is the cumulative difference between amortized and true cost: \(\Phi_i = \Phi_{i-1} + a_i - c_i\). If we can find an \(a_i\) such that \(\Phi_i \geq 0\) for each i, then we say the amortized cost is an upper bound on the true cost. And if the true cost is upper bounded by a constant, then we've shown that it is on average constant time.
- Steps:
Lecture 19 2018/03/05
- Dynamic connectivity
- Disjoint Sets ADT
1
2
3
4
5
6public interface DisjointSets {
/** Connects two items P and Q */
void connect(int p, int q);
/** Checks to see if two items are connected. */
void isConnected(int p, int q);
} - Implementation of disjoint sets
Map<Integer, Set>int[]
- QuickFind implementation
- Implementation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24public class QuickFindDS implements DisjointSets {
private int[] id;
public QuickFIndDS(int N) {
id = new int[N];
for (int i = 0; i < N; i++) {
id[i] = i;
}
}
public void connect(int p, int q) {
idp = id[p];
idq = id[q];
for (int i = 0; i < N; i++) {
if (id[i] == idp) {
id[i] = idq;
}
}
}
public boolean isConnected(int p, int q) {
return id[p] == id[q];
}
} - Performance analysis:
- Constructor: \(\Theta (N)\)
- isConnected: \(\Theta (1)\)
- connect: \(\Theta (N)\)
- Implementation
- QuickUnion implementation
- Implementation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26public class QuickUnionDS implements DisjointSets {
private int[] parent;
public QuickUnionDS(int N) {
for (int i = 0; i < N; i++) {
parent[i] = i;
}
}
private int find(int p) {
while (p != parent[p]) {
p = parent[p];
}
return p;
}
public void connect(int p, int q) {
rootp = find(p);
rootq = find(q);
parent[rootp] = rootq;
}
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
} - Performance analysis:
- Constructor: \(\Theta (N)\)
- isConnected: \(O (N)\)
- connect: \(O (N)\)
- Weighted QuickUnion
- Track tree size(number of elements)
- New rule: always link root of smaller tree to larger tree
- Max depth of any item is \(logN\)
- Implementation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39public class WeightedQuickUnionDS implements DisjointSets {
private int[] parent;
private int[] size;
public WeightedQuickUnionDS(int N) {
parent = new int[N];
size = new int[N];
for (int i = 0; i < N; i++) {
parent[i] = i;
size[i] = 1;
}
}
private int find(int p) {
while (p != parent[p]) {
p = parent[p];
}
return p;
}
private void connect(int p, int q) {
rootp = find(p);
rootq = find(q);
if (rootp == rootq) {
return;
}
if (size[rootp] < size[rootq]) {
parent[rootp] = rootq;
size[rootq] += size[rootp];
} else {
parent[rootq] = rootp;
size[rootp] += size[rootq];
}
}
private boolean isConnected(int p, int q) {
return find(p) == find(q);
}
} - Performance
- Constructor: \(\Theta (N)\)
- isConnected: \(O(logN)\)
- connect: \(O(logN)\)
- Path compression: replace
parent[i]with its foot for each i- Implementation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41public class WeightedQuickUnionWithPathCompressionDS implements DisjointSets {
private int[] parent;
private int[] size;
public WeightedQuickUnionWithPathCompressionDS(int N) {
parent = new int[N];
size = new int[N];
for (int i = 0; i < N; i++) {
parent[i] = i;
size[i] = 1;
}
}
private int find(int p) {
if (p == parent[p]) {
return p;
} else {
parent[p] = find(parent[p]);
return parent[p];
}
}
private void connect(int p, int q) {
rootp = find(p);
rootq = find(q);
if (rootp == rootq) {
return;
}
if (size[rootp] < size[rootq]) {
parent[rootp] = rootq;
size[rootq] += size[rootp];
} else {
parent[rootq] = rootp;
size[rootp] += size[rootq];
}
}
private boolean isConnected(int p, int q) {
return find(p) == find(q);
}
} - Performance analysis:
- Constructor: \(\Theta (N)\)
- isConnected: \(O(logN)\)
- connect: \(O(logN)\)
- Implementation
- Performance analysis(Runtime needed to perform M operations on a
DisjointSet object with N elements):
- QuickFind: \(O(MN)\)
- QuickUnion: \(O(MN)\)
- WeightedQuickFind: \(O(N+MlogN)\)
- WeightedQuickUnion: \(O(N+M \alpha N)\)
- Implementation
- Disjoint Sets ADT
Lecture 20 2018/03/17
- Binary Search Trees
- Definitions: A tree consists of a set of nodes and a set of edges that connect those nodes. There is exactly one path between any two nodes
- Related terminologies: root, child, parent, leaf, binary tree(child ranges from 0 to 2)
- BST property: For each node X in the tree
- Each key in the left subtree is less than X's key
- Each key in the right subtree is greater than X's key
- Orders must be complete, transitive and antisymmetric(no duplicative keys are allowed)
- Search operations
- Steps
- If searchKey eauals label, return
- If searchKey < label, search left subtree
- If searchKey > label, search right subtree
- Pseudo code
1
2
3
4
5
6
7
8
9
10
11
12public static BST find(BST T, Key searchKey) {
if (T == null) {
return null;
}
if (searchKey.compareTo(T.label) == 0) {
return T;
} else if (searchKey.compareTo(T.label) < 0) {
return find(T.left, searchKey);
} else {
return find(T.right, searchKey);
}
} - For a BST with N nodes, the worst time for search is \(logN\)
- Steps
- Insert operations
- Steps
- Search for key, if found, do nothing
- If not found, create a new node and set an appropriate link
- Pseudo code
1
2
3
4
5
6
7
8
9
10
11
12public static BST insert(BST T, Key insertKey) {
if (T == null) {
return new BST(insertKey);
}
if (insertKey.compareTo(T.label) < 0) {
T.left = insert(T.left, insertKey);
} else if (insertKey.compareTo(T.label) > 0) {
T.right = insert(T.right, insertKey);
}
// this means insertKey.compareTo(T.label) == 0
return T;
}
- Steps
- Delete operations
- Deletion key has no children: simplye remove the parent's link
- Deletion key has one children: point parent's link to child
- Deletion key has two children: replce key with predecessor(the rightmost key in left subtree) or successor(the leftmost key in right subtree), this is called Hibbard deletion
- For insertion operations, the tree can be around height of , but there is no way to maintain a satisfactory tree height for deletion operations
Lecture 21 2018/03/09
- Tree Rotation
- BST can be too to to be inefficient
- Tree rotation:
- Can shorten a tree
- Preserves BST property
- Rotation allows to balance each BST
- Rotate after each insertion and deletion to maintain balance
- B-trees/2-3 trees/ 2-3-4 trees
- Search trees
- BST: requires rotations to maintain balance. Many strategies for rotation(AVL, weight-balancing, red-black)
- Treaps
- Splay trees
- 2-3/2-3-4 trees/B-trees: no rotations required
- 2-3 trees
- There are 2-nodes and 3-nodes
- If a node is overstuffed, give the middle key of the node to parent
node, if parent node is overstuffed, then we need to split the parent
node
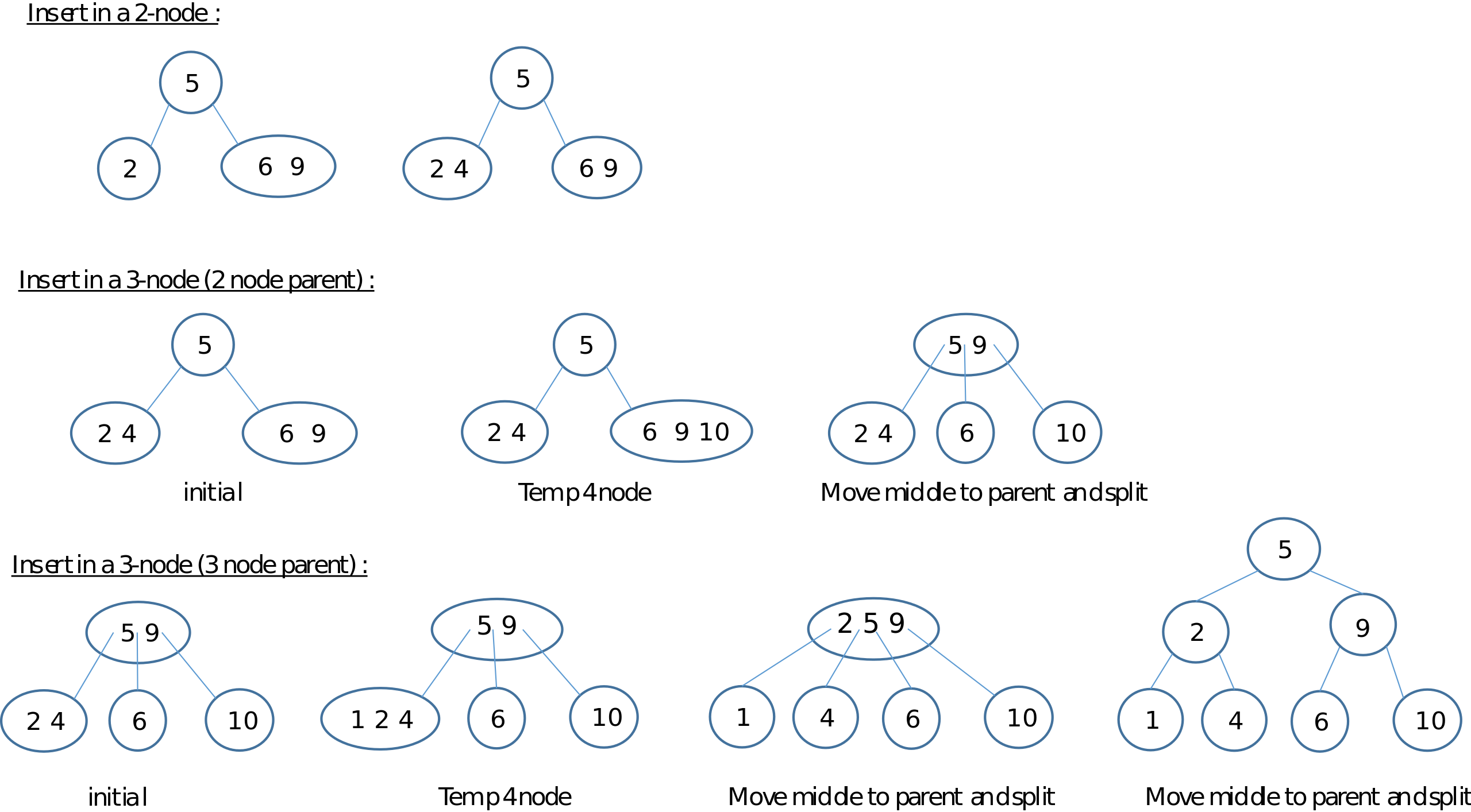
- 2-3-4 trees
- There are 2-nodes, 3-nodes and 4-nodes
- If we split the root, every node gets pushed down by exactly one level, if we split a leaf node or internal node, the height doesn't change
- All operations have guaranteed \(\Theta (logN)\) time
- If \(M\) is the max number of children, then the height of splitting trees should between \(log_M N\) and \(log_2 N\)
- B-trees
- A B-tree of order \(M = 4\) is also called a 2-3-4 tree or a 2-4 tree
- A B-tree of order \(M = 3\) is also called a 2-3 tree
- When M is very large, B-trees are used in practice for databases and filesystems
- B-trees are balanced
- Red-Black Trees
- 2-3/2-3-4 trees are a real pain to implement, and suffer from performance problems
- BST require rotations to maintain balance. 2-3/2-3-4 trees are balanced, no ratations requried.
- Build a BST that is isometric to a 2-3/2-3-4 tree: use rotations to ensure the isometry, since 2-3/2-3-4 trees are balanced, rotations on BST will ensure balance
- For 2-3 trees with only 2-nodes, the BST is the identical
- For 2-3 treew with 3-nodes, there could be different approaches
- Dummy glue nodes:
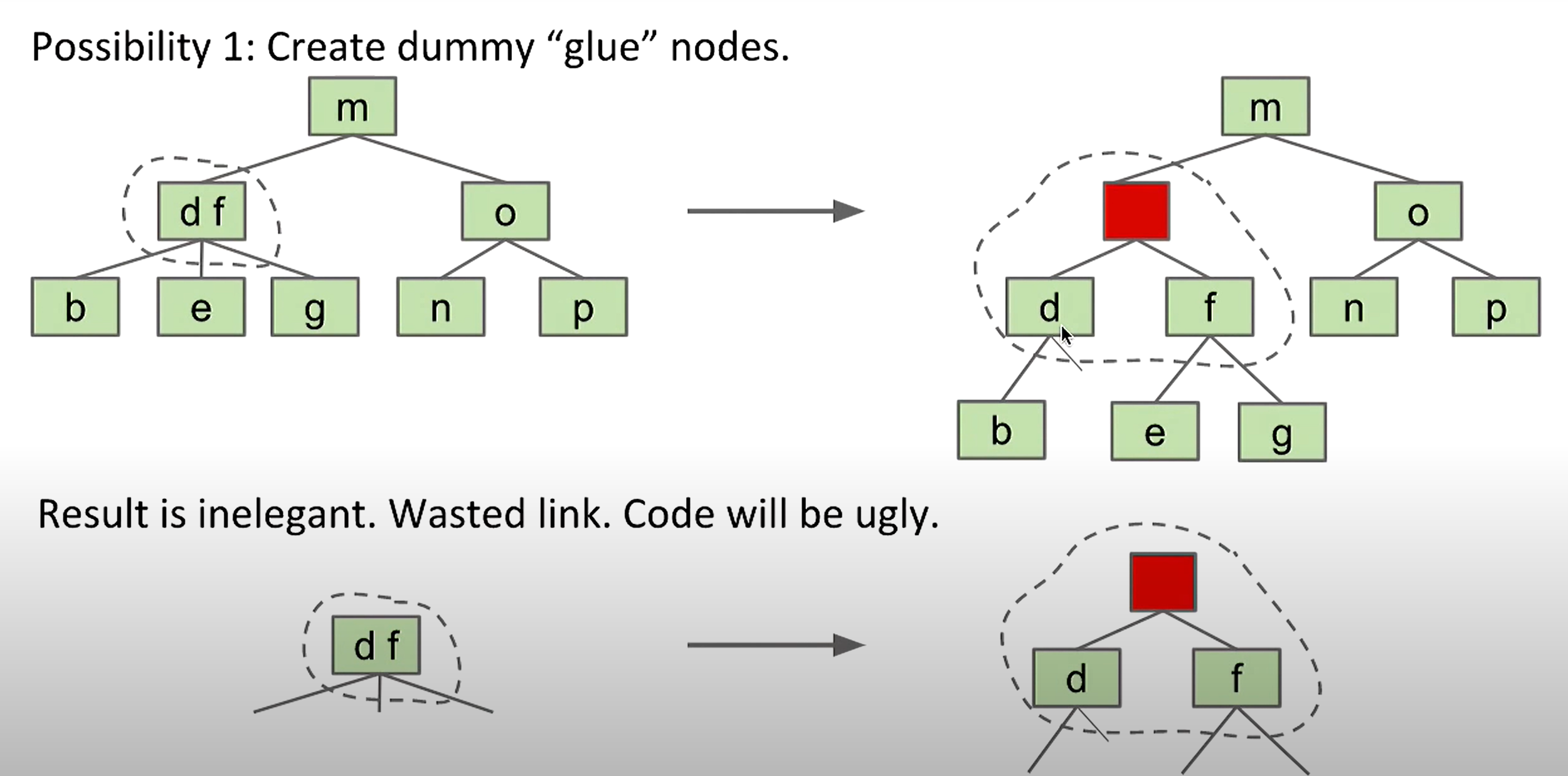
- Split 3-nodes with glue red links(commonly used, e.g.
java.util.TreeSet)
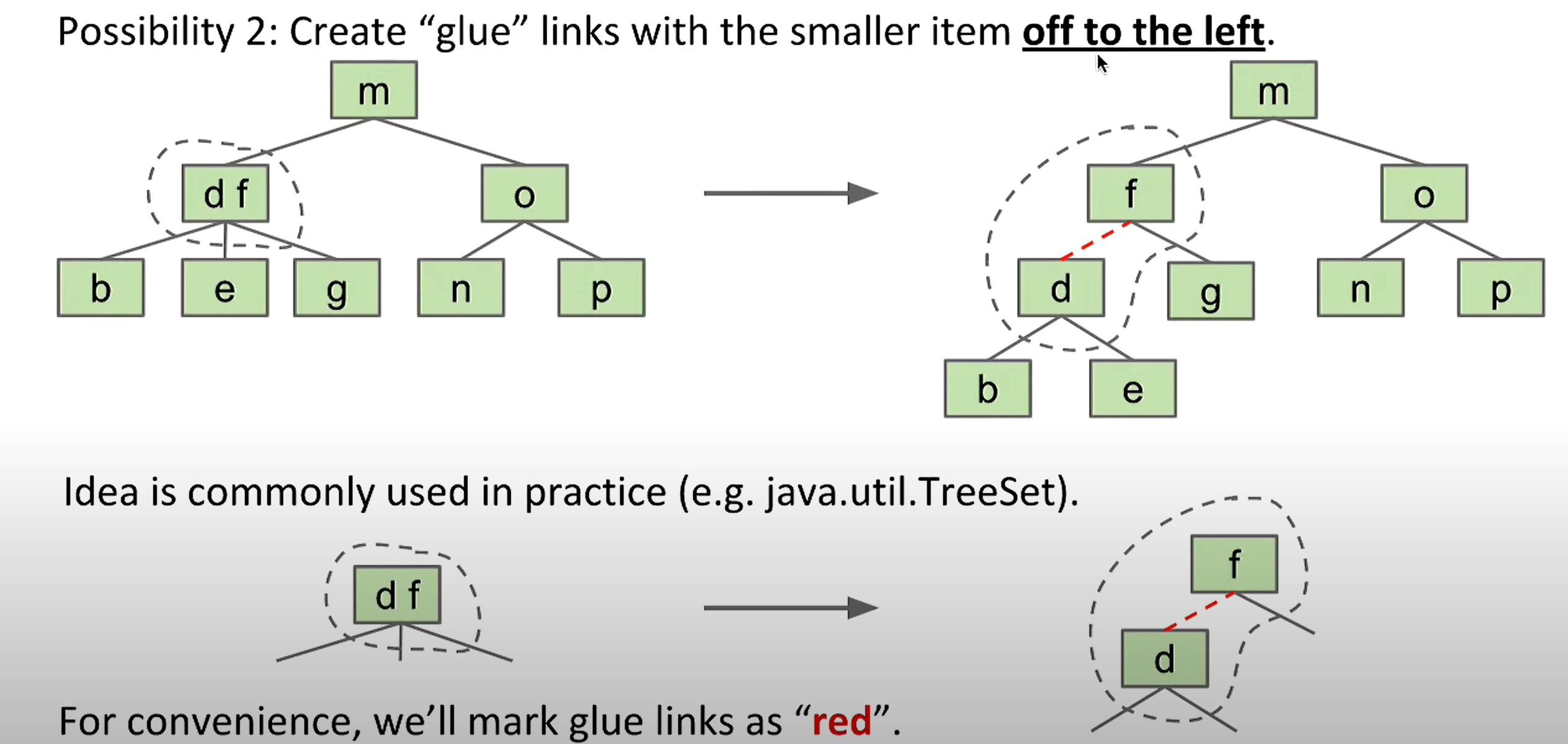
- Dummy glue nodes:
- LLRB(Left-leaning Red Black Binary Search Tree)
- No node has two red linkes
- Every path from root to a leaf has same number of black links
- Red links lean left
- For any 2-3 tree, the height of the associated LLRB is no more than twice of the original height of the 2-3 tree
- Search trees
Lecture 22 2018/03/12
- Rushy BST
- It can be used for storing data
- Limitations
- Items must be comparable
- Maintain balancing can be costly
- Efficiency: \(\Theta (logN)\), be we can do better
- The approach
- All data is just a sequence of bits. Can treat key as a gigantic number and use it as an array index
- We need collision handling and a straightforward hashCode function
- Hash Table with External Chaining
containsfunction and insert function can be \(\Theta (Q)\), where \(Q\) is the longest length of the chains- If \(N\) items are inserted into \(M\) buckets, the average runtime growth will be \(N/M = L\), also known as the load factor, then the every operation is \(\Theta (L)\)
- When \(L\) is small, the operations are fast, in order to maintain efficiency, we need to resize the buckets when there are more items
- Since hashCode can be negative, we need to use hashCode % length + length as the index
- Hash Functions
- We want a hash functions that can spread the items
- Example \[h(s)=s_0 31^{n-1}+s_1 31^{n-2}+\dots +s_{n-1}\]
- The Object class uses the address of an item as its hashCode
- If you overwite the equals function, you must overwrite the hashCode function at the same time
Lecture 23 2018/03/14
- Priority Queue
- Interface
1
2
3
4
5
6
7
8
9
10public interface MinPQ<Item> {
// Adds the item to the priority queue
public void add(Item x);
// Returns the smallest item in the priority queue.
public Item getSmallest();
// Removes the smallest item in the priority queue.
public Item removeSmallest();
// Returns the size of the priority queue.
public int size();
} - Application: monitor user's messages and find the unhamorious ones
- Naive way: put all messages into a list and sort with a comparator
- Priority Queue way: only maintain the M(a user-defined criterion) most unhamorious messages with a priority(if size is larger than M, simply call removeSmallest function)
- Interface
- Implementations of MinPQ
Comparisons
Ordered Array Bushy BST Hash Table Heap add \(\Theta (N)\) \(\Theta (log N)\) \(\Theta (1)\) \(\Theta (logN)\) getSmallest \(\Theta (1)\) \(\Theta (log N)\) \(\Theta (N)\) \(\Theta (N)\) removeSmallest \(\Theta (N)\) \(\Theta (log N)\) \(\Theta (N)\) \(\Theta (log N)\) Heap
- Binary min-heap: Binary tree that is complete and obeys min-heap
property:
- Min-heap: every node is less than or equal to both of its children
- Completeness: missing items only at the bottom level(if any), all nodes are as far left as possible
getSmallest(): simply return the root of the heapremoveSmallest():- Swap the last item and the root
- Sink down the current root item
insert(Item x):- Add the item to the last of the heap temporarily
- Pop up the item if needed to maintain the min-heap property
- Binary min-heap: Binary tree that is complete and obeys min-heap
property:
Tree Representation
- Approach 1: Create mapping from node to children
- Approach 1A: Fixed-width tree
1
2
3
4
5
6public class Tree<Key> {
Key key;
Tree left;
Tree middle;
Tree right;
} - Approach 1B: Variable-Width Tree
1
2
3
4public class Tree<Key> {
Key key;
Tree[] children;
} - Approach 1c: Sibling Tree
1
2
3
4
5
6
7public class Tree<Key> {
Key key;
// The link that points to a child
Tree favoredChild;
// The link that points to a sibling
Tree sibling;
}
- Approach 1A: Fixed-width tree
- Approach 2: Store keys in an array, store parentIDs in an array
1
2
3
4
5public class Tree<Key> {
Key[] keys;
// parents[i] = j means the parent of node i is node j
int[] parents;
} - Approach 3: Store keys in an array, don't store structure anywhere,
simply assume tree is complete(does not work for incomplete trees)
- Approach 3A: Indexing from 0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18public class Tree<Key> {
Key[] keys;
public void popUp(int k) {
if (keys[parent(k)] > keys[k]) {
swap(k, parent(k));
popUp(parent(k));
}
}
public int parent(int k) {
if (k == 0) {
return 0;
} else {
return (k - 1) / 2;
}
}
} - Approach 3B: Store by 1 offset, indexing from 0,but data is stored
starting from 1, leftChild(k) = k * 2, rightChild(k) = k * 2 + 1,
parent(k) = k / 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14public class Tree<Key> {
Key[] keys;
public void popUp(int k) {
if (keys[parent(k)] > keys[k]) {
swap(k, parent(k));
popUp(parent(k));
}
}
public int parent(int k) {
return k / 2;
}
}
- Approach 3A: Indexing from 0
- Approach 1: Create mapping from node to children
Lecture 24 2018/03/16
- Use BSTs to build Sets and Maps, use Heaps to build PQs
- Traversals
- Level order traversals
- Travel top-to-bottom, lefti-to-right
- Nodes are visited in the given order
- Lever order Traversal with Iterative Deepening
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17public void leverOrder(BSTNode x, Action toDo) {
for (int i = 0; i < T.height(); i++) {
visitLevel(T, i, toDo);
}
}
public void visitLevel(BSTNode x, int level, Action toDo) {
if (T == null) {
return;
}
if (level == 0) {
toDo.visit(x.key);
} else {
visitLevel(x.left, level - 1, toDo);
visitLevel(x.right, level - 1, toDo);
}
} - Iterative deepening runtime for a complete BST of height \(logN\) is \(\Theta (N)\), and the runtime for a spindly BST of height \(N\) is \(\Theta (N^{2})\)
- Depth First Traversals:
- Preorder, inorder, postorder
- Basic idea: traverse deep nodes before shallow ones, this is a recursive process
- If time needed to visit each node is constant, then the time of whole traversal is \(\Theta (N)\)
- Preorder traversal
1
2
3
4
5
6
7
8
9preOrder(BSTNode x) {
if (x == null) {
return;
}
// Do something with the key
System.out.println(x.key);
preOrder(x.left);
preOrder(x.right);
} - Inorder traversal
1
2
3
4
5
6
7
8
9public void inOrder(BSTNode x) {
if (x == null) {
return;
}
inOrder(x.left);
//Do something with the key
System.out.println(x.key);
inOrder(x.right);
} - Postorder traversal
1
2
3
4
5
6
7
8
9public void postOrder(BSTNode x) {
if (x == null) {
return;
}
postOrder(x.left);
postOrder(x.right);
//Do something with the key
System.out.println(x.key);
} - A trick for the map of the BST(draw the tree with root on the top,
then travel from top-to-bottom and left-to-right):
- Preorder traversal: each time on the left side of the node, mark it as visited
- Inorder traversal: each time on the bottom of the node, mark it as visited
- Postorder traversal: each time on the right side of the node, makr
it as visited
- Level order traversals
- Range Finding
- We want search like public Set
- Obviously we can use DFS to do this, but we can use pruning to speed up the process
- Pruning: restrict our search to only nodes that might contain the answers we seek
- With pruning, the runtime can be \(\Theta(logN + R)\), where \(R\) is the number of matches
Lecture 25 2018/03/21
Graphs
- Graph: a set of nodes(called vertices) connected pairwise by edges
- Terminologies: vertices, edges, dajacent vertices, vertices or edges may have labels(weights), path, cycle, connected vertices
- Some graph problems:
- s-t Path: is there is a path between s and t
- Shortest s-t Path: what is the shortest path between s and t
- Cycle: does the graph contain any cycles
- Euler tour: is there a cycle that uses every edge exactly once
- Hamilton tour: is there a cycle that uses every vertex excatly once
- Connectivity is the graph conencted, i.e. is there a path between all vertex pairs
- Biconnectivity: is there avertex whose removal disconnect the graph
- Planarity: can you draw the graph on a piece of paper with no crossing edges
- Isomorphism: are two graphs isomorphic(the same graph in
disguise)
Graph Representations
- Common convention: use number throughout the graph implementation
- Graph API
1
2
3
4
5
6
7
8
9
10
11
12public class Graph {
// Create empty graph with v vertices
public Graph(int V);
// add edge v-w
public void addEdge(int v, int w);
// vertices adjacent to v
Iterable<Integer> adj(int v);
// number of vertices
int V();
// number of edges
int E();
} - Representations
- Adjacent matrix: printing graph costs \(\Theta (N^2)\) time
- Edge sets: (source, target) sets
- Adjacency lists: the most common approach. Efficiency analysis for printing graph, best case \(\Theta (V)\), worst case \(\Theta (V^2)\), all cases \(\Theta (V+E)\)
- Adjacency list implementation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21public class Graph {
private int final V;
private List<Integer>[] adj;
public Graph(int V) {
this.V = V;
adj = (List<Integer>[]) new ArrayList[V];
for (int v = 0; v < V; v++) {
adj[v] = new ArrayList<Integer>();
}
}
public void addEdge(int v, int w) {
adj[v].add(w);
adj[w].add(v);
}
public Iterable<Integer> adj(int v) {
return adj[v];
}
} - Comparisons
idea addEdge(s, t)for(s: adj(v))printgraph()hasEdge(s, t)space used adjacency matrix \(\Theta (1)\) \(\Theta (V)\) \(\Theta (V^2)\) \(\Theta (1)\) \(\Theta (V^2)\) list of edges \(\Theta (1)\) \(\Theta (E)\) \(\Theta (E)\) \(\Theta (E)\) \(\Theta (E)\) adjacency list \(\Theta (1)\) \(\Theta (1)\) to \(\Theta (1)\) \(\Theta (V+E)\) \(\Theta (degree(v))\) \(\Theta (V+E)\) Depth First Traversal
- Maze traversal/s-t Path
- We need to ensuer we will no be lost in an infinite loop, so an array for marking the visited vertices is needed
- Algorithms:
- Mark s
- If s == t, return True
- Check all of s's unmarked neighbors for connectivity to t
- DFS implementation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37public class Paths {
// If s and t and connected, then marked[v] is true
private boolean[] marked;
// edgeTo[v] is the previous vertex of v on the path from s to v
private int[] edgeTo;
private final int s;
public Paths(Graph G, int s) {
this.s = s;
edgeTo = new int[G.V()];
marked = new boolean[G.V()];
dfs(G, s);
}
private void dfs(Graph G, int v) {
marked[v] = true;
for (int w: G.adj(v)) {
if (! marked[w]) {
edgeTo[w] = v;
dfs(G, w);
}
}
}
public boolean hasPathTo(int v) {
return marked[v];
}
public Iterable<Integer> pathTo(int v) {
if (!hasPathTo(v)) {
return null;
}
Stack<Integer> path = new Stack<Integer>();
for (int x = v; x != s; x = edgeTo[x]) {
path.push(x);
}
path.push(s);
return path;
}
}
- Maze traversal/s-t Path
Lecture 26 2018/03/23
- epth First Path
- DFS is a more general term for any graph search algorithm that traverses a graph as deep as possible begore backtracking
- Rumtime: \(\Theta (V+E)\), space \(\Theta (V)\)
- Preorder DFS on a graph: order of dfs calls
- Post order DFS on a graph: order of returns from dfs
- Level order DFS on a graph: order of increasing distance from s
- Topological Sort
- Definition: a topological sort of a directed graph is a linear ordering of its vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering
- The algorithm:
- Perform a DFS traversal from every vertex with indegree 0, not
clearing markings in between traversals
- Record DFS post order in a list
- Topological ordering is given by the reverse of that list(to avoid reversing a list, you can simply use a stack instead)
- Perform a DFS traversal from every vertex with indegree 0, not
clearing markings in between traversals
- The implementation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27public class DepthFirstOrder {
private boolean[] marked;
private Stack<Integer> reversePostorder;
public DepthFirstOrder(Digraph G) {
reversePostorder = new Stack<Integer>();
marked = new boolean[G.V()];
}
for (int v = 0; v < G.V(); v++) {
if (!marked[v]) {
dfs(G, v);
}
}
private void dfs(Digraph G, int v) {
marked[v] = true;
for (int w: G.adj(v)) {
if (!marked[w]) {
dfs(G, w);
}
}
reversePostorder.push(v);
}
public Iterable<Integer> reversePostorder() {
return reversePostorder;
}
} - Runtime: \(\Theta (V+E)\), space: \(\Theta (V)\)
- readth First Search
- For trees, we use iterative deepening, although it's bad for spindly trees(\(\Theta (N^2)\))
- BFS algorithm:
- Initiate a queue with a starting vertex s and mark that vertex
- Repeat until queue is empty:
- Remove vertex v from queue
- For each unmarked neighbor of v: mark, add to queue, set its edgeTo = v
- Implementation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26public class BreadthFirstPaths {
private boolean[] marked;
private int[] edgeTo;
public BreadthFirstPaths(Graph G, int s) {
marked = new boolean[G.V()];
edgeTo = new int[G.V()];
bfs(G, s);
}
private void bfs(Graph G, int s) {
Queue<Integer> fringe = new Queue<Integer>();
fringe.enqueue(s);
marked[s] = true;
while (!fringe.isEmpty()) {
int v = fringe.dequeue();
for (int w: G.adj(v)) {
if (!marked[w]) {
fringe.add(w);
marked[w] = true;
edgeTo[w] = v;
}
}
}
}
} - Runtime: \(\Theta (V+E)\), space: \(\Theta (V)\)
- We can use BFS for shortest path
Lecture 27 2018/04/02
- For connectivity problem, if the graph is bushy, BFS can be slower, while for spindly graph, DFS may perform worse
- For unweighted graph, BFS is goold for shortest path, but for weighted graph, we need to use Dijkstra's algorithm(BFS find path with least vertices, but such a path may not be the shortest)
- Djikstra's algorithm
- Single source single target shortest path problem, the solution is always a path with no cycles(if a graph has no cycles and each node has one parent, then it's a tree)
- Consider the shortest path tree of a connected edge-weighted graph(assume ever vertex is reachable), the edges of the SPT is always \(V-1\), since all nodes in the tree has one parent(then one edge) except for the root
- Algorithm: visit vertices in order of best-known distance from the
source vertex, relaxing each edge from the visited vertex(relax an edge:
add to SPT if better distane)
- Insert all vertices into fringe PQ, storing vertices in order of distance from source(initial distTo = \(+\infty\))
- Repeat until fringe PQ is emtpy: remove nearest vertices in the PQ, relax all edges(update distTo and edgeTo, and reorder in the PQ)
- Implementation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58public class DijkstraSP {
private double[] distTo; // distTo[v] = distance of shortest s->v path
private DirectedEdge[] edgeTo; // edgeTo[v] = last edge on shortest s->v path
private IndexMinPQ<Double> pq; // priority queue of vertices
public DijkstraSP(EdgeWeightedDigraph G, int s) {
distTo = new double[G.V()];
edgeTo = new DirectedEdge[G.V()];
for (int v = 0; v < G.V(); v++)
distTo[v] = Double.POSITIVE_INFINITY;
distTo[s] = 0.0;
pq = new IndexMinPQ<Double>(G.V());
pq.insert(s, distTo[s]);
while (!pq.isEmpty()) {
int v = pq.delMin();
for (DirectedEdge e : G.adj(v))
relax(e);
}
}
private void relax(DirectedEdge e) {
// edge from tail to head, node.from returns the tail, node.to returns the head, and tail.weight() returns the weight
int v = e.from();
int w = e.to();
if (distTo[w] > distTo[v] + e.weight()) {
distTo[w] = distTo[v] + e.weight();
edgeTo[w] = e;
if (pq.contains(w)) {
// distTo[w] decreas, so we need to find a correct place for it
pq.decreaseKey(w, distTo[w]);
} else {
pq.insert(w, distTo[w]);
}
}
}
public double distTo(int v) {
validateVertex(v);
return distTo[v];
}
public boolean hasPathTo(int v) {
return distTo[v] < Double.POSITIVE_INFINITY;
}
public Iterable<DirectedEdge> pathTo(int v) {
validateVertex(v);
if (!hasPathTo(v)) return null;
Stack<DirectedEdge> path = new Stack<DirectedEdge>();
for (DirectedEdge e = edgeTo[v]; e != null; e = edgeTo[e.from()]) {
path.push(e);
}
return path;
}
} - Runtime: \(O((V+E)logV)\)
- \(A^{*}\) Algorithm
- If we have an estimate of the distance between the origin and single target, then seraching from the nearest vertex will not be a good idea. In such a situation we use \(A^{*}\) algorithm instead in which we order the vertices using \(distTo(v) + h(v)\), where \(h(v)\) is an estimate of the distance of v
- We first make out a heuristic \(h(v)\) for each vertex v and calculate \(distTo(v) + h(v)\) instead of \(distTo(v)\) in the Dijkstra's algorithm
- A heuristic that overestimates is inadmissible, as long as the heuristic is admissible, the \(A^*\) algorithm can yield the shortest path
Lecture 28 2018/04/04
- Check is there is a cycle in a graph:
- DFS: runtime check vertices, \(\Theta (V+E)\)
- QuickUnionUF: check edges, runtime \(\Theta (V +ElogV)\)
- Spanning Tree:
- Definition: given an undirected graph, a spanning tree T is a subgraph of G, where T: is connected, is acyclic, includes all of the vertices
- A minimum spanning tree is a spanning tree with minimum total weight
- MSP v.s. SPT
- The SPT depends on the start vertex, but MSP does not
- The MST sometimes happens to be an SPT for a specific vertex(it's no guaranteed that the MST can be a SPT of a specific vertex)
- The cut property
- A cut is an assignment of a graph's nodes to two non-empty sets
- A crossing edge is an edge which connects a node from one set to a node frmo the other set
- Given a cut, minimum weight crossing edge is in the MST(can be proved by contradiction)
- Prim's algorithm
- Steps:
- Start fron some arbitrary node, add shortest edge(this is a shortest crossing edge) that has one node inside the MST under construction, repeat until V - 1 edges
- Prim's algorithm and Dijkstra's algorithm are actuall the same, except Dijstra's algorithm considers distance from the source, and Prim's algorithsm considers distance from the tree
- Implementation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66public class PrimMST {
private Edge[] edgeTo; // edgeTo[v] = shortest edge from tree vertex to non-tree vertex
private double[] distTo; // distTo[v] = weight of shortest such edge
private boolean[] marked; // marked[v] = true if v on tree, false otherwise
private IndexMinPQ<Double> pq;
public PrimMST(EdgeWeightedGraph G) {
edgeTo = new Edge[G.V()];
distTo = new double[G.V()];
marked = new boolean[G.V()];
pq = new IndexMinPQ<Double>(G.V());
for (int v = 0; v < G.V(); v++) {
distTo[v] = Double.POSITIVE_INFINITY;
}
for (int v = 0; v < G.V(); v++) {
if (!marked[v]) {
prim(G, v);
}
}
}
private void prim(EdgeWeightedGraph G, int s) {
distTo[s] = 0.0;
pq.insert(s, distTo[s]);
while (!pq.isEmpty()) {
int v = pq.delMin();
scan(G, v);
}
}
private void scan(EdgeWeightedGraph G, int v) {
// v is in the MST
marked[v] = true;
for (Edge e : G.adj(v)) {
// the other end of the edge e
int w = e.other(v);
if (marked[w]) {
continue;
}
if (e.weight() < distTo[w]) {
distTo[w] = e.weight();
edgeTo[w] = e;
if (pq.contains(w)) {
pq.decreaseKey(w, distTo[w]);
} else {
pq.insert(w, distTo[w]);
}
}
}
}
public Iterable<Edge> edges() {
Queue<Edge> mst = new Queue<Edge>();
for (int v = 0; v < edgeTo.length; v++) {
Edge e = edgeTo[v];
if (e != null) {
mst.enqueue(e);
}
}
return mst;
}
} - Runtime: \((V+E)logV\)
- Steps:
- Kruskal's Algorithm
- Algorithm: consider edges in order of increasing weight, add to MST unless a cylce is created, repeat until V - 1 edges. We can do this by firstly inserting all edges into the PQ, and then repeatedly removing the smallest weight edge and adding it to the MST if no cycing is created
- The MST under construction in Prim's algorithm is always conencted, but the one in Kruskal's algorithm needs not to be connected
- The implementation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41import java.util.Arrays;
public class KruskalMST {
private double weight; // weight of MST
private Queue<Edge> mst = new Queue<Edge>(); // edges in MST
public KruskalMST(EdgeWeightedGraph G) {
// create array of edges, sorted by weight
Edge[] edges = new Edge[G.E()];
int t = 0;
for (Edge e: G.edges()) {
edges[t++] = e;
}
Arrays.sort(edges);
// run greedy algorithm
UF uf = new UF(G.V());
for (int i = 0; i < G.E() && mst.size() < G.V() - 1; i++) {
Edge e = edges[i];
int v = e.either();
int w = e.other(v);
// v-w does not create a cycle
if (uf.find(v) != uf.find(w)) {
uf.union(v, w); // merge v and w components
mst.enqueue(e); // add edge e to mst
weight += e.weight();
}
}
}
public Iterable<Edge> edges() {
return mst;
}
public double weight() {
return weight;
}
} - Runtime: \(ElogE\)
Lecture 29 2018/04/06
- MSP for DAG
- DAG: directed acyclic graph, any such graph can be topological sorted(sometimes called linearization)
- Dijkstra's algorithm on DAG: visit the vertex in the topological
order and relax all of its going edges
- Runtime: \(\Theta (E+V)\)
- Dynamic Programming:
- Definition: the approach of solving increasingly large subproblems is called dynamic programming
- The longest increasing subsequence: given a sequence of integers,
find the longest increasing subsequence(LIS), or the length of the
longest increasing subsequence(LLIS)
- Approach 1:
- Create a DAG with the integers, and find the longest path, the vertices in the path construct the LIS
- The algorithm:
- Create copy with edge weights set to -1
- For each vertex v:
- Run DAGSPT algorithm from v, let LP[v] = abs(min(disTo(w)))
- Return max(LP), then the longest path should start from that vertex
- Runtime: \(\Theta (N^3)\)
- Approach 2:
- Let LLSEA(k) be the length of longest subsequence ending at index k, for abbreviation, we denote it as Q(k)
- The algorithm:
- Q = [0, Double.NEGATIVE_INFINITY, ..., Double.NEGATIVE_INFINITY]
- For each k = 1, ..., N: if there exists an L such that Q[L] + 1 > Q[k], then Q[k] = Q[L] + 1, otherwise Q[k] = 1
- Return max(Q)
- Runtime: \(\Theta (N^3)\)
- Approach 1:
Lecture 30 2018/04/09
- Sorting
- A osrt is a permutation of a sequence of elements that brings them
into order according to some total order. A total order is:
- Totao: \(x \leq y\) or \(y \leq x\) for all x, y
- Reflexive: \(x \leq x\)
- Antisymmetrix: \(x \leq y\) and \(y \leq x\) iff \(x=y\) (x and y are equivalent)
- Transitive: \(x \leq y\) and \(y \leq z\) implies \(x \leq z\)
- In java, total order is specified by compareTo or compare methods, it may be inconsistent with equals method
- An inversion is a pair of elements that are out of order
- Time complexity: the runtime efficiency of an algofithm
- Space complexity: extra memory usage of an algorithm
- A osrt is a permutation of a sequence of elements that brings them
into order according to some total order. A total order is:
- Selection Sort and Heap Sort
- Selection Sort
- Selection sroting N items
- Find the smallest item in the unsorted portion of the array
- Move it to the end of the sorted portion of the array
- Selection sort the remaining unsorted items
- Runtime: \(\Theta (N^2)\)
- Selection sroting N items
- Naive Heapsort
- Naive Heapsort using a max-oriented heap:
- Insert the N items from an input into a max-heap, this costs \(\Theta (NlogN)\)
- Delete the max item from the heap and insert it into the output array, selecting the largest is \(\Theta (1)\) and removeing the largest is \(\Theta (logN)\)
- The total runtime for the above heapsort is \(O(NlogN)\), the space complexity is \(\Theta (N)\)
- Naive Heapsort using a max-oriented heap:
- Inplace Heapsort
- Use bottom-up heapification to convert the input array into a heap,
this costs \(O(NlogN)\)
- Sink every node in reverse level order(from the back of the array, that is, the last item in the heap)
- After sinking, it is guaranteed that tree rooted at position k is a heap, when the tree at root is a heap, then the entire tree is a heap
- Delete the max from the heap and insert it into the back of the input array(keep reheaping during the process)
- The overall runtime is \(O(NlogN)\), space is \(O(1)\)
- Use bottom-up heapification to convert the input array into a heap,
this costs \(O(NlogN)\)
- Top-Down Merge Sort
- Top-Down merge sorting N items:
- Split items into 2 roughly even pieces
- Mergesort each half
- Merge the two sorted halves to form the final output
- Runtime: \(\Theta (NlogN)\), space \(\Theta (N)\)
- It's possible to do inplace merge sort, but the performance is terriable
- Top-Down merge sorting N items:
- Insertion Sort
- Not inplace version:
- From leftmost part of the input array
- Add each item from input, inserting into output at right point
- Inplace version:
- Repeat for i = 0 to N - 1:
- Designate item i as the traveling item
- Swap item backwards until traveller is in the right place among all previously examined items(do this with two pointers)
- Runtime: \(\Theta (1)\) for best case, \(O(N^2)\) for worst case, for small arrays(N < 15) or arrays with a small number of inversions, insertion sort is fast
- Repeat for i = 0 to N - 1:
- Not inplace version:
- Selection Sort
Lecutre 31 2018/04/11
- Quick Sort
- Partition: the partition of an array
a[]on elementx = a[i]is to rearrancea[]so that:- x moves to position j(may be the same as i)
- All entries to the left of x are \(\leq x\)
- All entries to the right of x are \(\geq x\)
- Dutch flag problem:
- Naive approach: create another array and copy the items
- Another approach: two pointers
- Runtime for the best case \(\Theta (NlogN)\), and the worst case one is \(\Theta (N^2)\), runtime for the average case is \(\Theta (NlogN)\). While for merge sort, both best case and worst case runtime are \(\Theta (NlogN)\)
- Quick sort is actually a BST sort
- Avoid worst cases:
- Worst case examples:
- Bad ordering: array already in sorted order
- Bad elements: array with all duplicates
- Strategies:
- Randomness: pick a random pivot or shuffle before sorting
- Smarter pivot selection: calculate or approximate the median
- Introspection: switch to a safer sort if recursion goes too deep
- Preprocess the array: analyze to see if quick sort is appropriate
- Worst case examples:
- Partition: the partition of an array
Lecture 32 2018/04/13
- Speed up quick sort
- Choose correct pivot
- Choose correct partition algorithm
- Try to avoid worst cases
- Tony Hoare's Inplace Partition Scheme
- Pivot first item
- L pionter starts from leftmost, it loves smll items
- G pointer starts from rightmost, it loves large items
- L moves right, G moves left, they stop on disliked items, then swap item on L and G
- When L and G cross, stop the process
- Swap item at pivot and item at G
- The Quick sort widely used nowadays uses two pivots
- Quick Select
- Compute the exact median would be great for picking an item to partition around
- We can use partitioning to find the exact median, and the algorithm is the best known median identification algorithm
- Steps:
- Pick the leftmost item as pivot, then do partitioning
- The median should be at index arr.length / 2, so only need to repeat the process for one part
- Repeat until the median is found
- Stability, Adaptiveness, Optimization
- Stability
- Definition: a sort is said to be stable if order of equivalent items is preserved
- Summary
Memory Comlexity Notes Stable? Heap Sort \(\Theta (1)\) \(\Theta (NlogN)\) Bac caching No Insertion Sort \(\Theta (1)\) \(\Theta (N^2)\) \(\Theta (N)\) is almost sorted Yes Merge Sort \(\Theta (N)\) \(\Theta (NlogN)\) Yes Quick Sort \(\Theta (logN)\) \(\Theta (NlogN)\) Fatest sort No - Some tricks:
- Switch to insertion sort
- Make sort addaptive
- Arrays.sort()
- For primitive types: it uses quick sort to sort things in ascending numerical order
- For reference types: it uses merge sort to sort things in ascending order according to the natural order of items
- Shuffling
- Easiest way to shuffle an array:
- Associate each item with a random number
- Sort the items by the random number
- Easiest way to shuffle an array:
- Stability
Lecture 33 2018/04/16
- Some Math Problem
- \(N! \in \Omega ((N/2)^{N/2})\) (Consider Stirling's formula: \(N! = \sqrt{2 \pi N} (\frac{N}{e})^N\))
- \(logN! \in \Omega (NlogN)\) (This is obvious from the above equation)
- \(NlogN \in \Omega(logN!)\) (Again refer to the Stirling's formula, another way \(NlogN = logN + logN+\dots+logN\), \(logN!=logN+log{N-1}+\dots+log1\))
- Bounds
- If there is a clevest comparison based sorting algorithm, the upper bound runtime should be \(O(NlogN)\), because it should not be worse than merge sort
- The lower bound should be \(\Omega(N)\), because it should at least inspect all N items
- We can prove the lower bound should be \(\Omega(NlogN)\): there are \(N!\) permutations of the decision tree, so we need \(log{N!}\) height of the decision tree, so the lower bound is \(\Omega(log{N!})\)
- We can convert other kinds of problems into sorting problems. Then
the lower bound and higher bound of sorting also applies to other
problems
- Any comparison based sort needs at least \(NlogN\) comparisons
Lecture 34 2018/04/18
- Better asymptotic performance does not imply better real world performance
- Sleep sort:
- For each interger x in an array, sleep for x seconds and print x
- Runtime \(N+max(x)\)
- Counting sort:
- Count number of occurrences of each item
- Iterate through list, using counting array to decide where to put everything
- Runtime: \(\Theta (N+R)\), where \(R\) is the size of the counting array, memory usage: \(\Theta (N+R)\)
- LSD Radix sort
- LSD(least significant digit, the rightmost one)
- Sort each digit independently from rightmost digit towards left
- When keys are of different lengths, you can treat empty spaces as less than all other characters(simply you can treat them as 0)
- Runtime \(\Theta (WN+WR)\), where \(W\) is the width of the longest key
- For highly dissimilar strings: meerge sort wins over lsd sorts,
while for highly similar strings, the situation is vice versa
- MSD Radix sort
- MSD(most significant digit, the leftmost one)
- Key idea: sort each subproblem separately
- Runtime: best case \(\Theta (N+R)\), worst case \(\Theta (WN+WR)\)
Lecture 35 2018/04/20
- Trie: a digit-by-digit set representation
- Trie short for retrieval tree
- Pronounced same as tree
- Runtime: given with \(N\) keys and
a key with \(L\) digits, then
- Worst case insertion runtime: \(\Theta (L)\), (\(L+1\))
- Worst case search runtime: \(\Theta (L)\), (\(L\))
- Best case search runtime: \(\Theta (L)\), (search miss for the first digit)
- Runtime for Hash table search: \(\Theta (NL)\) for worst case, \(\Theta (L)\) typical case, \(\Theta (L)\) best case
- Comparisons in trie are done digit-by-digit, allowing us to skip some characters
- Usage: asymptotic speed improvement is nice, but main appeal of
tries is their ability to support rapid prefix matching and approximate
matching:
- Finding all keys that match a given prefix
- Finding longest prefix of keys(prefix: a substring starting from root and ending with a possible ending point in the trie)
- Trie Implementation
- Naive way
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35public class TrieSet {
# Support characters up through 128
private static final int R = 128;
private class Node {
// If exists is true, this means it's an ending node.
boolean exists;
Node[] links;
public Node() {
links = new Node[R];
exists = false;
}
}
private Node root = new Node();
public void put(String key) {
put(root, key, 0);
}
private Node put(Node x, String key, int d) {
if (x == null) {
x = new Node();
}
if (d == key.length()) {
x.exists = true;
return x;
}
char c = key.charAt(d);
x.links[c] = put(x.links[c], key d + 1);
return x;
}
}
- Naive way
- Improvement of Trie
- Track children in a better way than with an array of length R
- Ternary Search Tries
- Patricia/Radix Tries
- DAWG
- Suffix/Prefix Array
Lecture 36 2018/04/23
- Compression
- In a lossless algorithm we require that no information is lost
- Text files often compressible by 70% or more
- Prefix Free Codes
- By default, English text is usually represented by sequences of characters, each 8 bits long
- We can use fewer than 8 bits for each letter
- For our normal situations, the binary code for one character can be prefirx for another character, so operators need to use a pause symbol between binary codes to avoid ambigunity
- We can remove ambigunity by useing prefix free codes, where no code is the prefix of another, so there is no pause needed
- Shannon-Fano code: a prefix-free based compression method
- Huffman code: bottom up approach using relative frequency as weight of an item